The stiffness of flat washers and Belleville springs was work out by General Motors engineers Almen and Laszlo in 1936. The equation derived show shim stiffness has a complex dependence on shim OD, ID, edge lift and thickness.

The additional function, f(d.od/d.id), is a long equation involving the ratio of the shim inside to outside diameter.

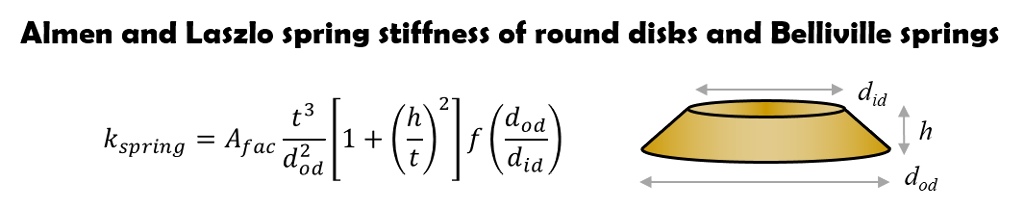
Shim factors simplify the Almen and Laszlo theory by estimating shim stiffness relative to the stiffness of a 0.1 mm thick reference shim. The reference 0.1 mm shim is defined to have the same diameter and reduced edge lift so the ratio of edge lift to thickness is the same (h/t).

Those simplifications cancel out all of the complex terms in the Almen and Laszlo equation making shim stiffness a simple function of thickness cubed.

The shim factor table above shows a 0.11 mm shim is equivalent to 1.3 0.1 mm shims. So if you had a stack of four 0.1 mm shims you could replace it with (4/1.3= 3.08) three 0.11 mm shims.

Likewise, a 0.2 mm shim is equivalent to eight 0.1 mm shims. So if you had a shim stack with eight 0.1 mm shims you could replace it with (8/8.0= 1) a single 0.2 mm shim.

Shim factor accuracy

The simplifications used in deriving shim factors require evaluation of shim stiffness at the same edge lift to thickness ratio (h/t).

Eight 0.1 mm shims are equivalent to one 0.2 mm shim, but the stiffness of the eight 0.1 mm shims is evaluated at an edge lift of 0.1 mm, while the 0.2 mm shims have an edge lift of 0.2 mm.

The desired application of shim factors is to compare shim stiffness at the same edge lift. At the same edge lift a 0.2 mm thick shim has 1/2 the (h/t) ratio of the reference 0.1 mm shim.

In the Almen and Laszlo equation, the edge lift ratio term (h/t) is squared resulting in a large effect on shim stiffness, which is one of the reasons why shim factors do not always give a reliable shim stiffness estimate.

MXScandinavia on Thumper Talk ran a series of dyno tests evaluating the accuracy of shim factors in estimating damping force changes. Some results were opposite of the expected change (more).