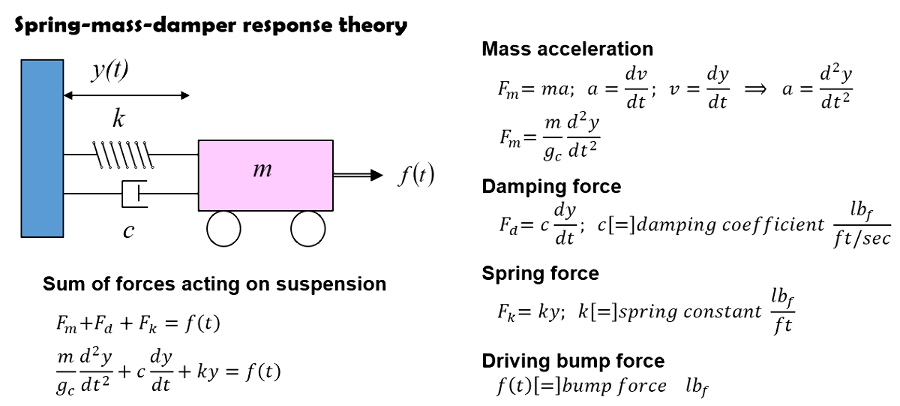
Spring-mass-damper theory applies the basic physics of F=ma to define suspension motion and response on bump impacts. Force (F) acting on the suspension is the combination of spring plus damping force. Mass (m) is the chassis or wheel weight depending on which body you want to look at. The combination of force and mass define the F=ma acceleration, which in turn defines the velocity, position and suspension response characteristics at any instant in time.
- Spring force: Spring force is defined by the spring constant (k) multiplied by the displacement (dy)
- Mass: Mass of the wheel or mass of the chassis. Spring-mass-damper theory describes motion of either body
- Damping: The shock absorber damping coefficient defined as damping force divided by shaft velocity. Damping linearly increases with shaft velocity
Spring-mass-damper theory applies the basic physics of F=ma to describe suspension motion
The three forces of spring, mass and damping completely describe suspension motion. Springs make the suspension bounce up and down. Damping stops the bouncing motion. There are no other forces acting on the suspension. In that sense the spring-mass-damper system equation provides an exact description of suspension motion.
Combining the above terms describing the forces acting on the suspension gives a single equation describing the F=ma suspension motion. The f(t) term is an arbitrary external force that kicks the suspension into motion, like hitting a bump.

Suspension response
The above equation can be solved analytically to obtain an exact mathematical equation describing the suspension position y(t) at any instant in time. The y(t) solution for an under damped suspension (zeta <1) is shown below.
The suspension velocity continuously changes through the stroke, which changes the damping force. The spring force also changes with stroke position. Multiple simultaneously changing forces makes it hard to guess the suspension motion.
Spring-mass-damper theory simplifies that complex problem identifying there are only two parameters that control suspension motion:
- tau defines the suspension oscillation frequency and the time required for the suspension to return to race sag.
- zeta describes how quickly oscillations damp.
The suspension motion equation describes the time required for the suspension to complete one oscillation cycle, which defines the suspension damped natural resonance frequency.

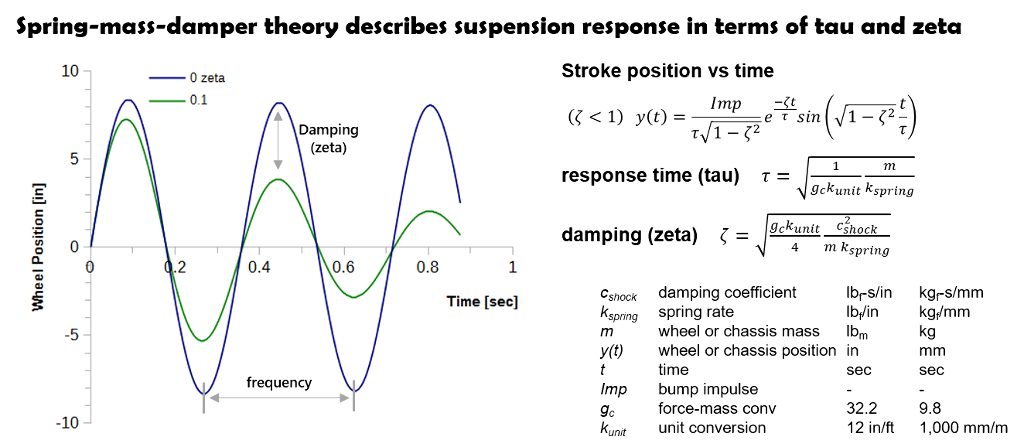
Any two suspensions, regardless of chassis weight, rider weight, spring rate or damping will give exactly the same response, retracing the curves above, if the values of tau and zeta are the same.
That fact from spring-mass-damper theory provides a powerful suspension tuning tool giving a direct way to scale suspension performance between different bikes.
Weight scaled suspension setups
Tau is simply the ratio of mass to spring rate. Weight [lbm] divided by spring rate [lbf/in] defines race sag. Setting race sag to the same target value on different bikes sets the first parameter needed to scale suspension setups.
Zeta defines damping. Zeta also includes mass and spring rate and adds the third parameter of damping in terms of the shock absorber damping coefficient (c). Tuning damping to match zeta sets the suspension response, “feel” and behavior to be the same on different suspension setups.
Those two parameters define the basis of weight scaling providing a powerful tuning tool allowing the performance of a known good suspension setup to be scaled across a wide range of bike weights, rider weights and spring rates.
The Shim ReStackor weight scaling spreadsheet is setup to make weight scaling easy. The single input of spring rate scales a known good damping curve to the spring rate and rider weight of a new setup. Tuning shock damping to match that target damping simply requires hacking around on the shock absorber shim stacks to hit the target damping curve (more).
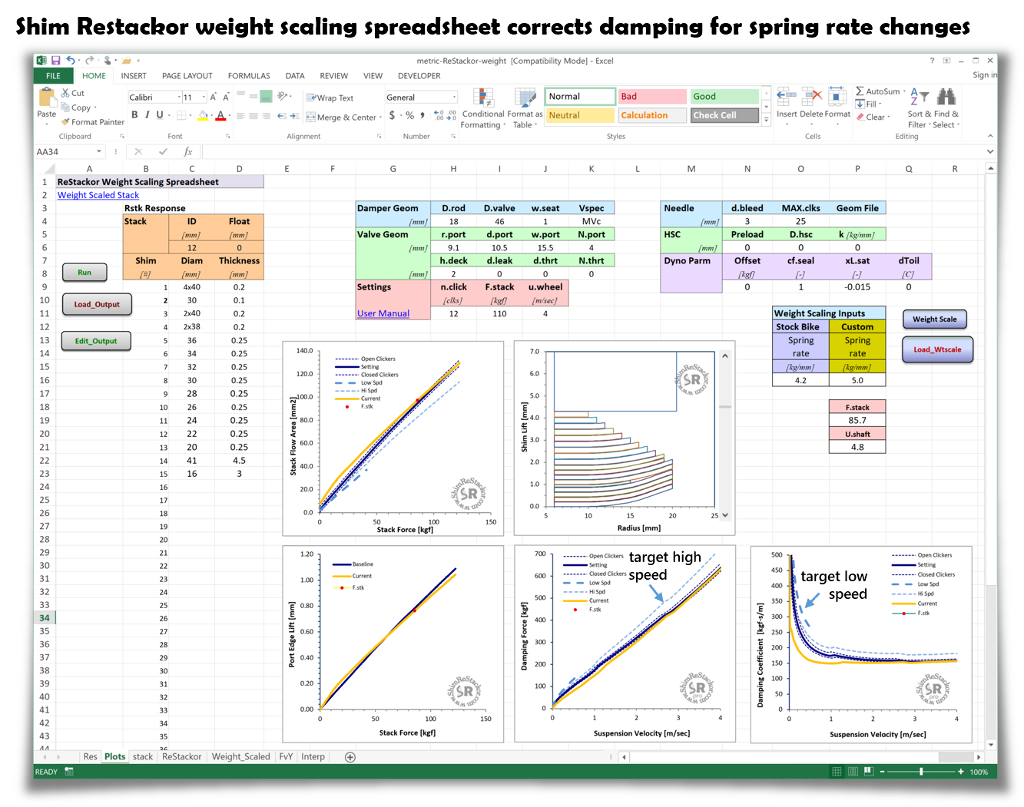
A second use of weight scaling is correcting stock damping for changes in rider weight and spring rate. Weight scaling stock damping provides a physics based method to correct damping for changes in spring rate and preserve the suspension response, “feel” and behavior the manufacturer intended for the bike.
Weight scaling the custom damping setup from your old bike to a new bike, correcting for differences in valve port geometry, bike weight and spring rate, duplicates performance of the original setup. Weight scaling gets you in the ballpark of a workable setup out of the box instead of spending weeks searching for a viable shim stack configuration.
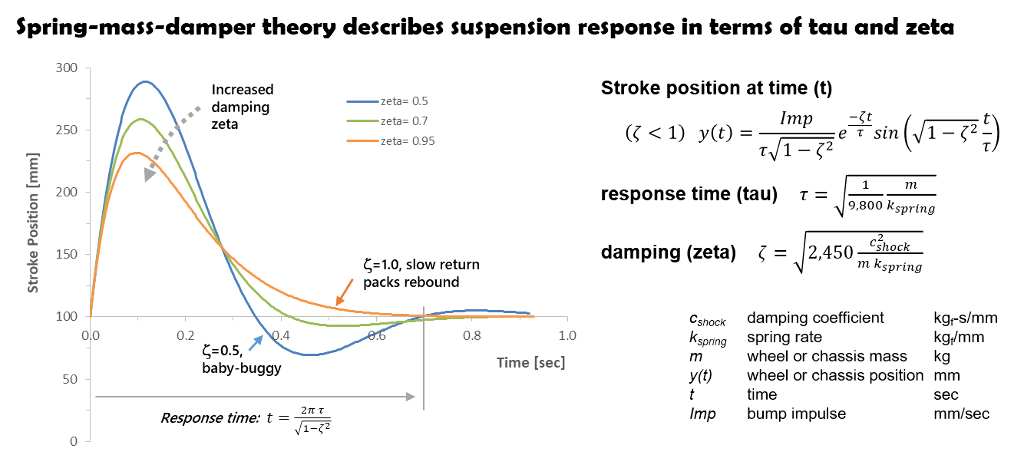
Spring-mass-damping theory defines damping in terms of zeta. Zeta values of 1.0 are critically damped meaning the suspension will not overshoot race sag or baby-buggy after a bump. No overshoot is desirable, however the stiff damping gives slow response causing rebound to pack on closely spaced bumps.
Lighter damping at zeta 0.5 returns the suspension to race sag faster, which reduces packing, but the residual suspension velocity on return to race sag causes the suspension to overshoot race sag and baby-buggy back. Baby-buggy motions of an underdamped suspension give poor “feel” making the suspension “feel” loose.
The worst possible scenario for a suspension is hitting the next bump while the suspension is still recovering from the previous bump. When that happens the bump impact augments the residual suspension motions from the previous bump driving the suspension into resonance.
Spring-mass-damper theory defines the damping stiffness required to suppress suspension resonance as zeta values of 1/sqrt(2)= 0.707 or higher.
That fact from spring-mass-damper theory uniquely defines zeta values of 0.707 to give the fastest possible rebound response (to prevent packing) with damping that is still stiff enough to suppress suspension resonance. Optimum rebound damping at zeta values of 0.7 has been verified through years of racing (more).
Spring-mass-damper theory
Suspension motions are complex. Spring-mass-damper theory breaks that complex problem down identifying two fundamental parameters that control suspension performance.
- Tau defines how long the suspension takes to return to race sag.
- Zeta defines how quickly oscillations damp.
Any suspension, regardless of weight, spring rate or damping, will give exactly the same response if the values of tau and zeta are the same.
Tuning damping in terms of zeta provides a direct method to scale suspension performance of a yz125 to a ktm950. When installing a 5.5 kg/mm spring you don’t have to guess how much damping is needed to control the stiffer spring. Zeta provides a direct method to compute the damping and get you in the ballpark of a good workable setup. That lets you focus on fine tuning the suspension instead of guessing where the ballpark of good damping might be.

