Bleed systems provide a controlled leak path bypassing the shim stack controlled valve. Bleed allows free return of the suspension to race sag on low speed suspension motions.
Suspension “feel” heavily depends on the control of low speed bleed systems. Numerous bleed systems are used in shock absorbers.

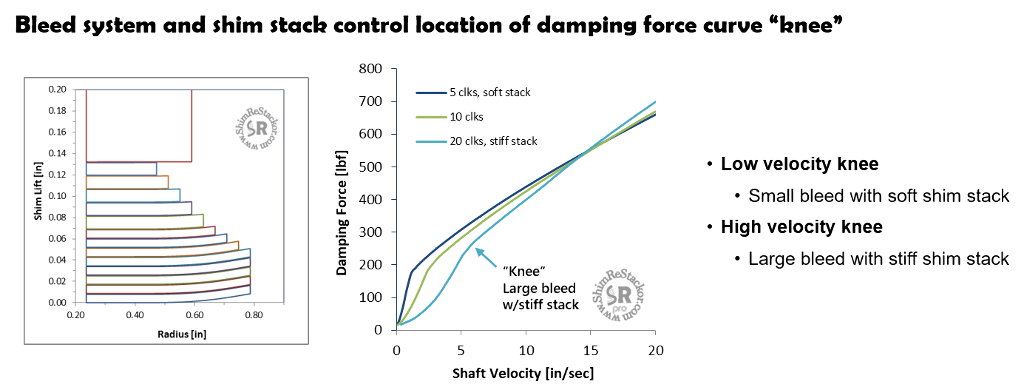
Damping curve knee
Clicker bleed circuits, leak jets, stack float or bleed shims all have a fixed constant area throat. Flow resistance through the throat is near zero at low speed and increases with velocity squared. The velocity squared pressure increase eventually produces enough backpressure to crack the shim stack open. Above the cracking pressure, digressive damping of the shim stack controlled valve controls the damping force curve shape.
The transition from velocity squared orifice damping to shim stack controlled digressive damping puts a “knee” in the damping force curve. The location of the “knee” is controlled by the bleed circuit flow area and stiffness of the shim stack.
Increasing the leak area provides more suspension compliance for rolling of trail trash. Decreasing the leak area provides more cornering “feel” and brake dive control.
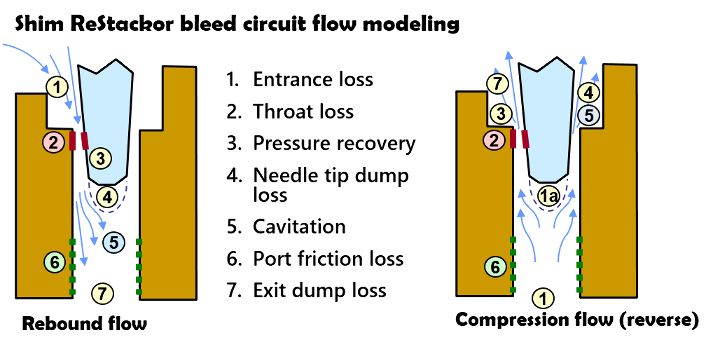
Clicker bleed circuits
The clicker bleed circuit is basically a needle valve. Accurate damping force calculations require a clicker needle geometry table to describe the needle taper. The geometry table is a simple listing of needle diameter as a function of clicker position. Details are listed in the User Manual.
Seven types of flow losses occur in the clicker bleed circuits. Due to the geometry, flow losses are slightly different in the forward and reverse (rebound) direction. (more).
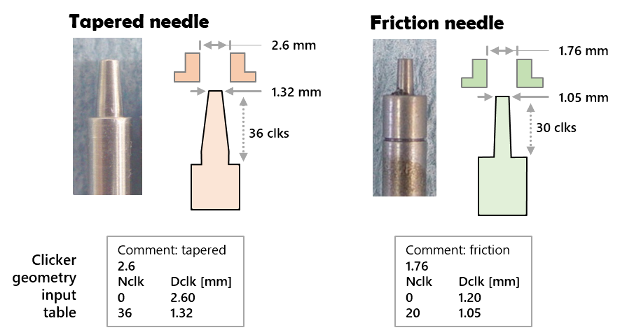
There are two basic styles of needles:
- Tapered needle: Screwing the needle in reduces the flow area
- Friction needle: Screwing the needle in increases the length of the high velocity throat increasing viscous friction losses
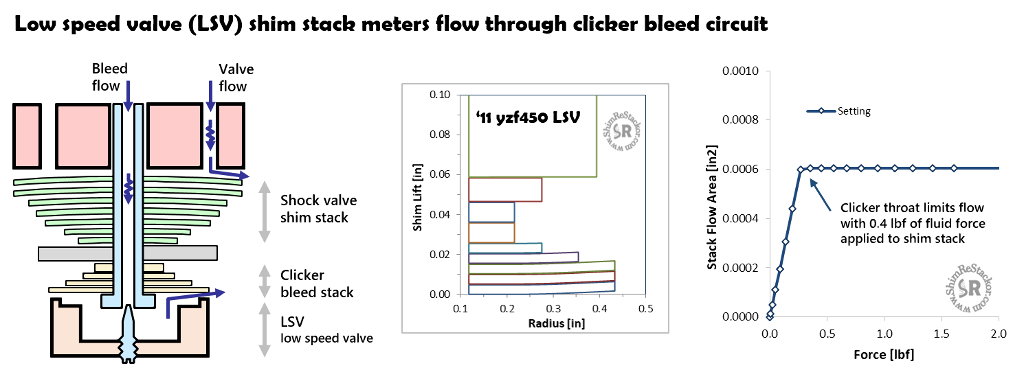
Low speed valve (LSV) shim stack
Low speed valve (LSV) refers to a shim stack on the clicker bleed circuit. Flow through the valve is small and limited by the clicker needle position. The LSV circuit is modeled in Shim ReStackor setting the valve port throat diameter (d.thrt) equal to the clicker needle flow area and modeling the shim stack in the usual way.
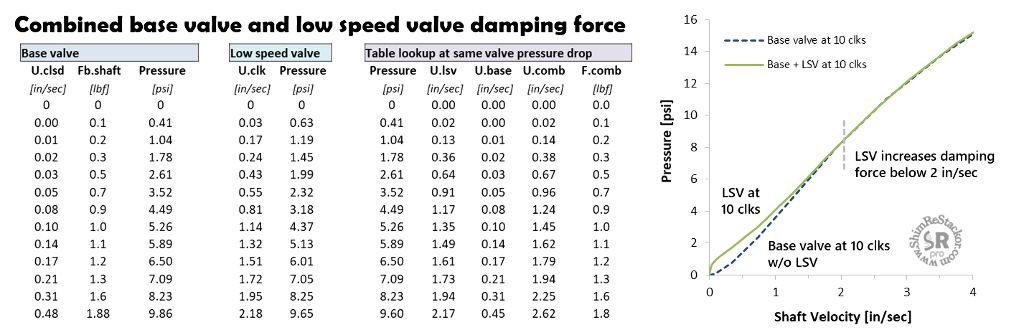
The example below computes the damping force for an ‘11 yzf450 fork base valve LSV circuit. With a fluid force of 0.4 lbf applied to the shim stack face the flow area through the LSV shim stack has deflected to the point where the clicker throat area limits the flow through the bleed circuit.
The LSV circuit creates two parallel fluid circuits through the fork base valve and LSV clicker circuit. Computing damping performance of the LSV circuit requires combining two separate Shim ReStackor calculations. The first calculation computes damping force through the base valve with the clickers closed. The second calculation computes damping force through the LSV circuit with the valve throat area set equal to the clicker throat area.
The two calculations are combined by selecting a sequence of progressively higher valve pressure drops and looking up the flow and shaft velocity through the base valve and the flow through the low speed valve at the same pressure drop. The total flow through the combined circuits is simply the sum of the two shaft velocities. At the selected valve pressure drop, the base valve damping force specifies the force on the shock shaft.
For the ‘11 yzf450 example, the LSV increases low speed damping by approximately 1 lbf up to shaft speeds of 2 in/sec. Above 2 in/sec the LSV shim stack has deflected to the point where the clicker throat limits the flow. Shim ReStackor calculations running the fork base valve only with clickers set at 10 out (dashed blue line) match the high speed LSV calculations since both are running the same bleed area.
Rebound separator valves on a shock operate in a similar fashion and primarily function as a check valve preventing reverse flow.
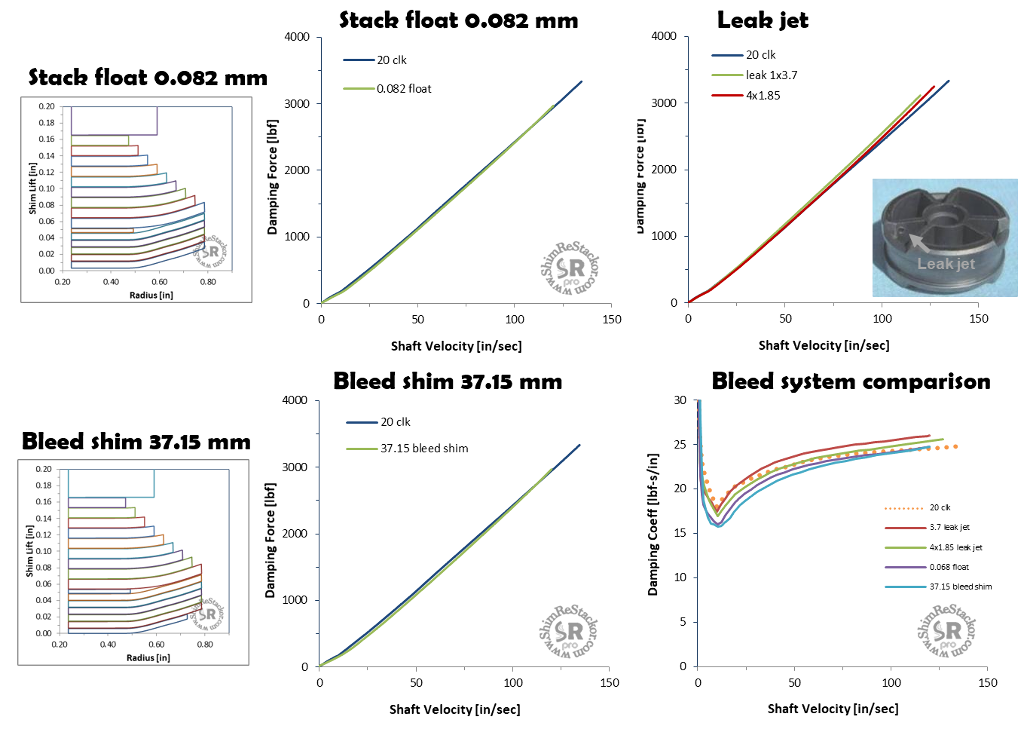
Stack float
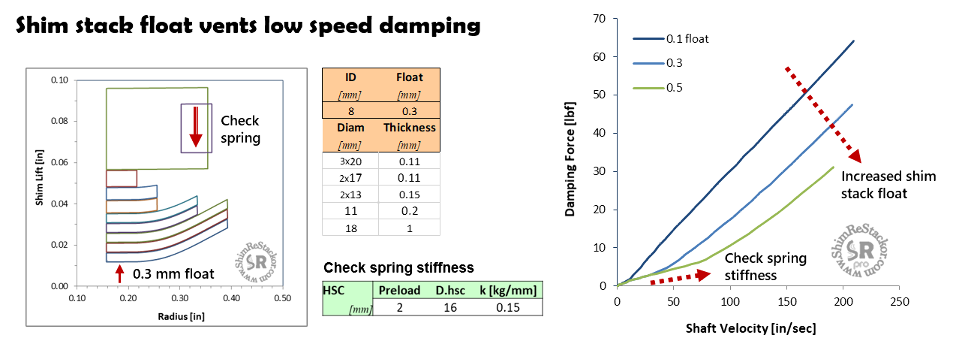
Float allows the shim stack to physically lift off of the valve face to vent low speed damping. The rate of float opening is controlled by the HSC spring stiffness input and the cracking pressure controlled by spring preload.
The “Float” input specifies the float travel limit. Beyond that limit, the shim stack clamp hits a hard stop and damping force is controlled by the stiffness and deflection of the shim stack (more).
Leak jets
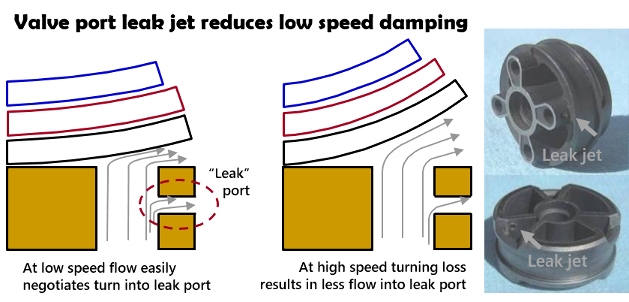
Leak jets are small holes drilled in the side of the valve port. Pressurized fluid in the valve port escapes through the leak jet venting low speed damping.
The 90 degree turn into the leak jet port reduces the flow effectiveness of leak jets at high speed.
Multiple leak jets
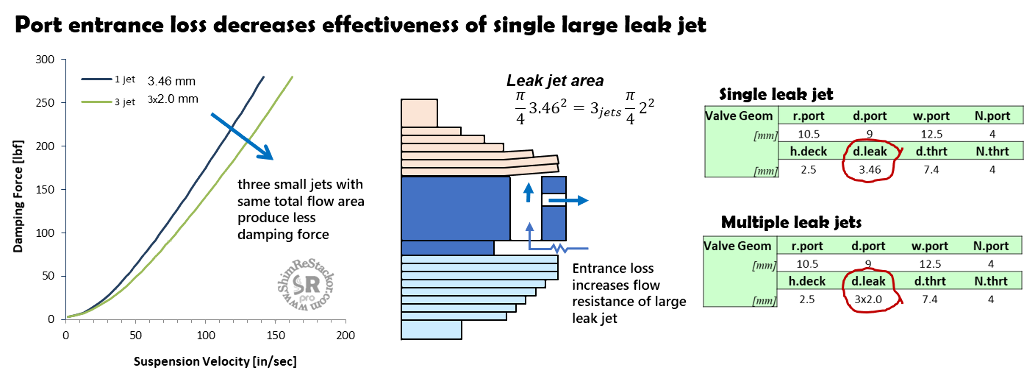
A single 3.46 mm diameter leak jet has the same flow area as three 2.0 mm jets. However, 2.0 mm leak jets installed on three ports produces a more effective bleed.
The difference is caused by flow losses at the port entrance. A single 3.46 mm leak jet increases the fluid flow through that single port, which increases flow losses at the port entrance.
Spreading the leak jet across three ports increases the flow through each port by a small amount and since flow losses increase with velocity squared, the small increase in entrance flow loss spread across three ports is less than the large increase on a single port.
A central focus of the physics based models of Shim ReStackor is application of the fundamental physics of fluid dynamics to account for multiple flow losses occurring in the shock fluid circuits both in series and in parallel. Those flow losses make the flow “effectiveness” of a single leak jet, multiple leak jets, bleed shims or clicker bleed all slightly different.
Reliable modeling shifts the focus from endless testing to simply hacking around on the number and diameter of leak jets until the desired damping force curve is achieved.
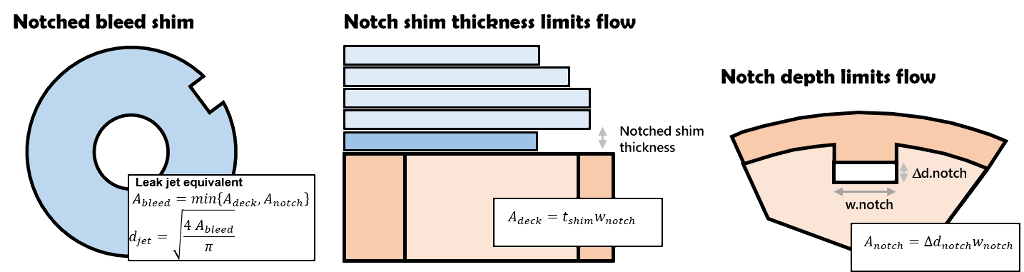
Notched bleed shims
Notched bleed shims provide a controlled leak at the valve face seat. The notch width, depth and shim thickness define the leak area.
The difference between the notch depth and valve seat diameter define the notch flow area (A.notch).
The notched shim thickness defines the dump flow area between the shim stack and valve deck (A.deck). The controlling bleed flow area is the minimum of the two.
Shim ReStackor models notched shims as a leak jet with the diameter defined by the minimum of A.notch or A.deck.
Bleed shim
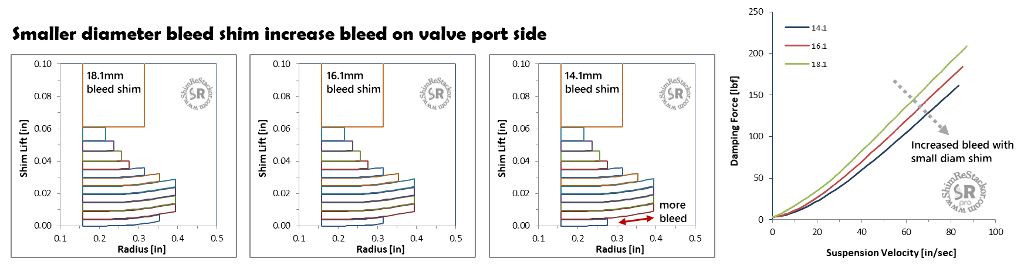
Shim stack face bleed shims are smaller than the valve port seat diameter. The smaller diameter face shim forms an edge gap defined by the bleed shim diameter and thickness.
Decreasing the bleed shim diameter increases the gap length along the valve port side providing more bleed and softer damping.
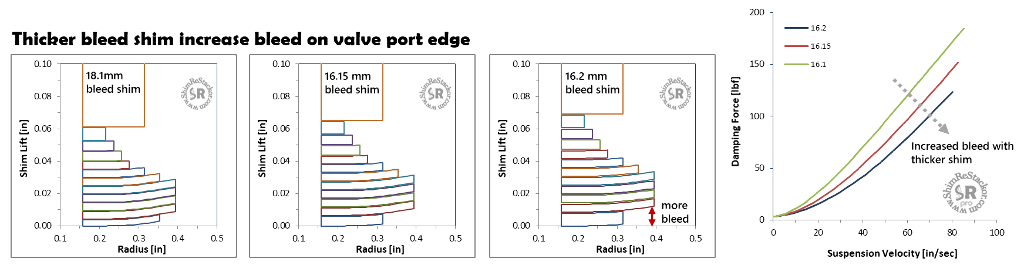
Increasing the bleed shim thickness increases the gap height at the valve port edge.
Thicker bleed shim increase the gap, giving more bleed flow area and softer damping.
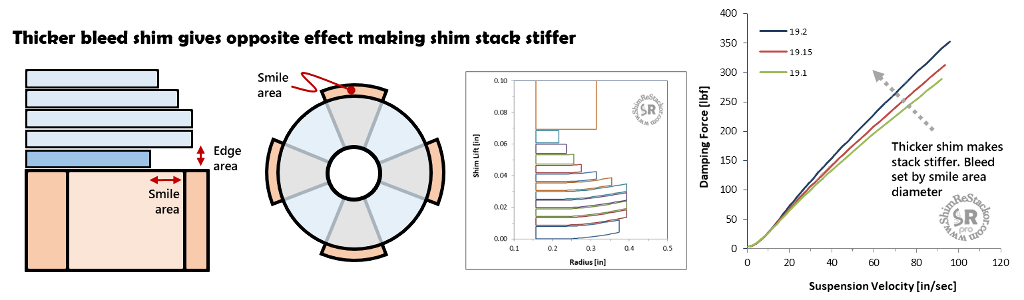
The example below shows the reverse effect where a thicker bleed shim increase damping force.
Bleed flow area is defined by two parameters: Edge flow area defined by shim thickness; Smile area defined by the shim and valve port diameter.
Smile area defines the bleed flow area for the large bleed shim diameter used in the example below. For that condition thicker shims make the shim stack stiffer and have no effect on bleed area.
Bleed system tuning
Notionally, 1.0 mm2 of bleed flow area through the clickers, leak jet, bleed shim, or stack float all produce the same effect. In detail, each circuit has a slightly different dependence on oil viscosity and density resulting in different bleed flow rates as the area is changed.
While those differences are real, they have little effect on tuning. For tuning, bleed circuits are simply modified - increasing or decreasing flow area - until the desired bleed effect is achieved.
That shifts the focus from trying to guess the bleed flow rate and range of shaft velocities influenced by bleed to computing the actual flow using Shim ReStackor. Tuning the shim stack and bleed circuits together as a system gives detailed fine tuning control of the shape of the damping force curve.
“Shim ReStackor: Fine tune your suspension setup far beyond the limits previously possible”
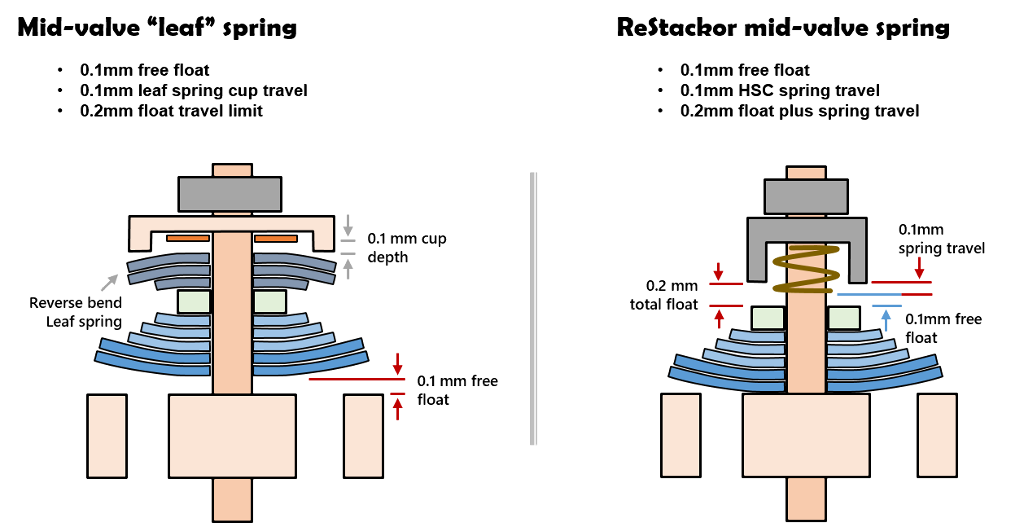
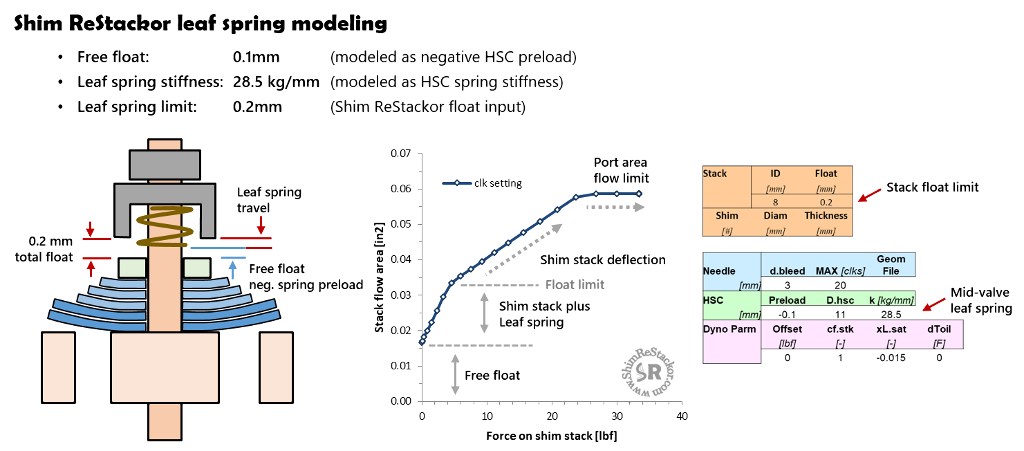
A fork midvalve “leaf-spring” is a stack of shims above the clamp that bend backward into the clamp washer cup, also known as a trampoline valve. Deflection of the leaf-spring floats the shim stack. Spacers in the cup limit the leaf-spring travel and the maximum stack float.
Shim ReStackor models leaf-springs using the high speed compression adjuster (HSC) inputs. Negative spring preload specifies free-float. The HSC coil spring stiffness specifies the stiffness of the leaf-spring and the shim stack float input specifies the max float travel where the leaf-springs bottom in the clamp washer cup.
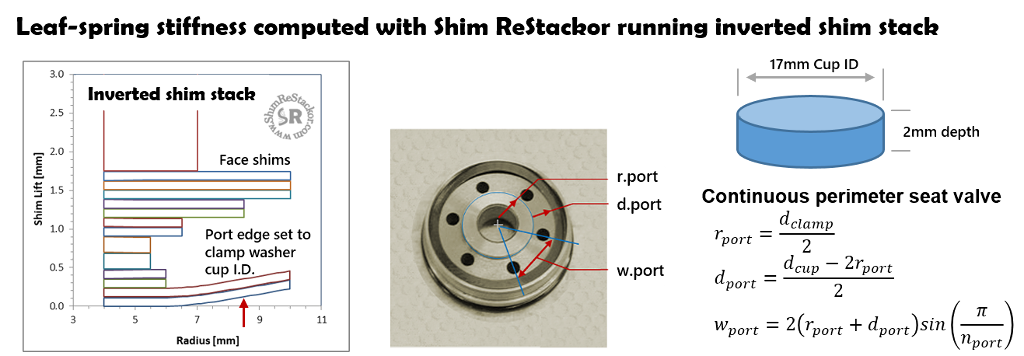
Leaf-spring stiffness
Stiffness of the reverse bend leaf-spring is determined running a separate Shim ReStackor calculation with the shim stack inverted. The inverted stack puts the leaf-springs on the valve face.
The valve is configured as a perimeter seat valve with the seat diameter matching the clamp washer cup. The stack clamp diameter of the leaf-spring defines r.port and the clamp washer cup radius defines r.port + d.port.
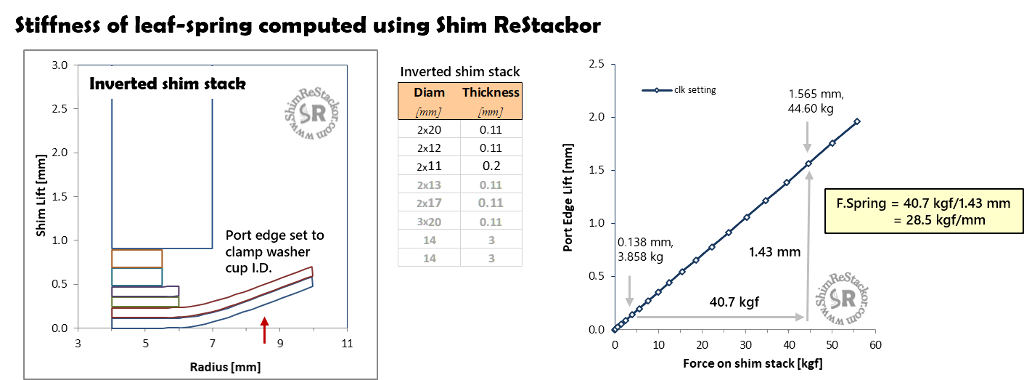
The port edge lift computed by Shim ReStackor gives a direct measure of leaf-spring stiffness. Over the 2mm of clamp washer cup travel the leaf-spring stiffness is nearly linear. Linear stiffness makes the HSC coil spring used in Shim ReStackor modeling a good approximation.
The spring rate of the leaf-spring is simply force divided by displacement. Picking points off of the computed port edge lift curve shows the leaf-spring stiffness is 28.5 kgf/mm.
Leaf-spring tuning
Three Shim ReStackor inputs define leaf-spring performance:
Negative spring preload: Negative preload allows the stack to free-float before engaging the HSC coil spring. In the example free float is 0.1 mm.
HSC spring stiffness: Deflection stiffness of the leaf-spring is modeled using the HSC coil spring.
Fluid force applied on the shim stack face compresses the HSC spring progressively increasing the shim stack float.
Float: The Shim ReStackor float input defines the travel limit. At the float travel limit, the stack clamp hits a hard stop equivalent to bottoming the leaf spring in the cup.
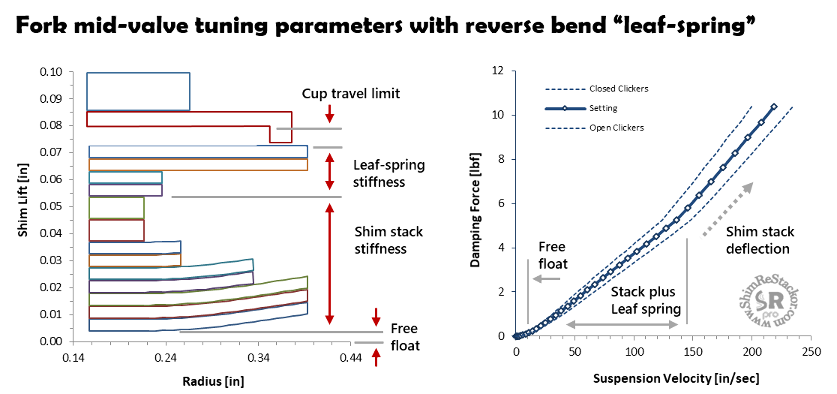
Fork mid-valve tuning
Free-float sets the suspension velocity where the mid-valve begins generating compression damping force. Free-float is set by negative HSC spring preload.
In the second range, the combined deflection of the shim stack and reverse bend leaf-spring controls the valve port flow area and damping force. Modifying the leaf spring stiffness controls the slope of the curve through the second range.
At 150 in/sec the leaf-spring bottoms in the clamp washer cup. The Shim ReStackor float input specifies the leaf-spring travel limit.
After the leaf spring bottoms, the deflection stiffness of the shim stack becomes the single parameter controlling flow area and damping force.
At ultra-high speed the valve port throat area limits the flow creating a fourth damping force range.
Shim ReStackor models all four ranges. Parameters controlling the start and end of each range are tunable as well as the damping force through each range. Leaf-springs can be tuned for control of low speed float as in the example or as a high speed blow-off system.
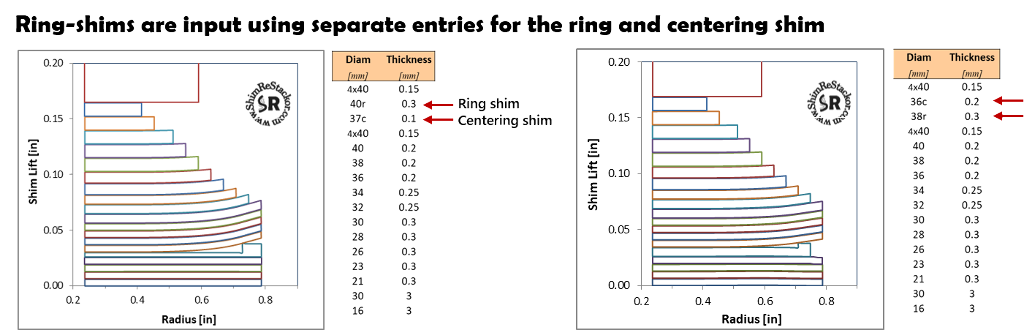
Ring shims have two parts: a centering shim and a thicker outside ring shim. The ring shim preloads the shim stack against the valve face requiring higher pressures to crack the shim stack open.
Shim ReStackor requires two inputs for ring shims. The centering shim is marked with the letter “c” and the thicker ring-shim is marked in a separate input with the letter “r”.
The centering shim can be listed first or second, the order does not matter.
Preload produced by the ring-shim can be tuned by changing the ring-shim thickness or the centering shim thickness. Preload can also be changed moving the ring shim up or down in the stack or by changing the ring shim diameter.
Ring shim tuning
Preload produced by ring-shims significantly increase damping force everywhere across the speed range. Chucking a ring-shim on an existing shim stack to see what it “feels” like on a test ride will give the result of “too stiff” everywhere.
To make ring-shims useful the shim stack has to be re-tuned to work with the ring-shim preload and increased low speed damping.
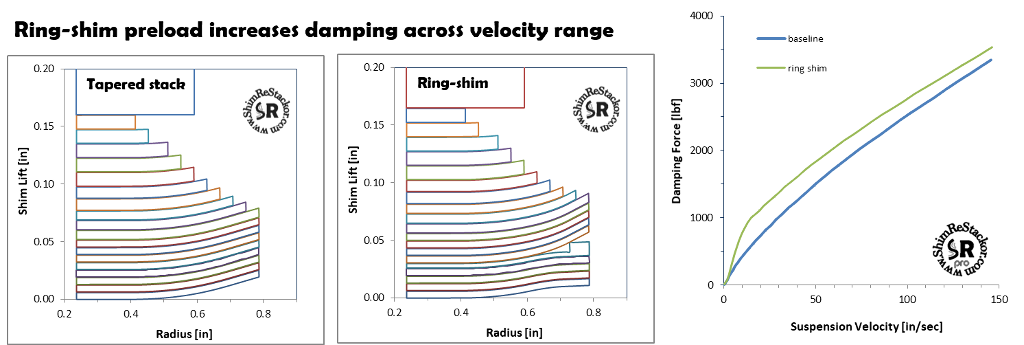
Increased low speed damping
Ring-shims are typically used to increase low speed damping. The example below softens the shim stack taper using thinner shims to compensate for the ring-shim addition.
The result is stiffer damping at low speed and the same damping at high speed.
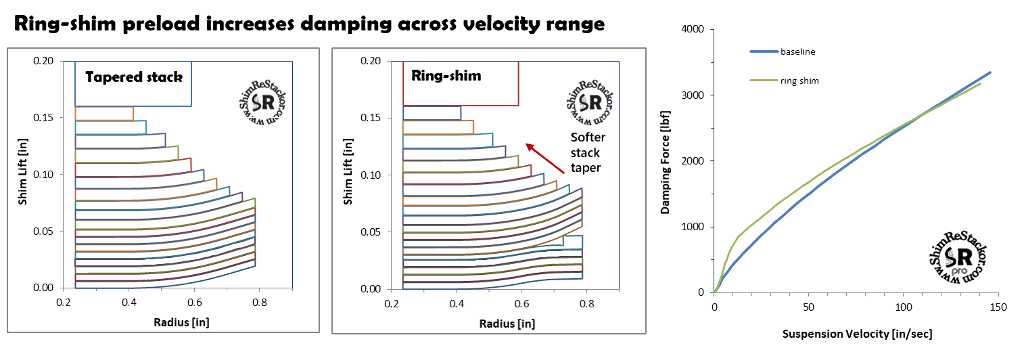
Reduced high speed damping
Ring shims can be tuned the other way around to soften high speed damping.
Adjusting ring-shim preload on a soft shim stack matches the low speed damping force of the original baseline stack.
When pushed to high speed, the softer shim stack produces less damping force giving the result of matched low speed damping and softer high speed.
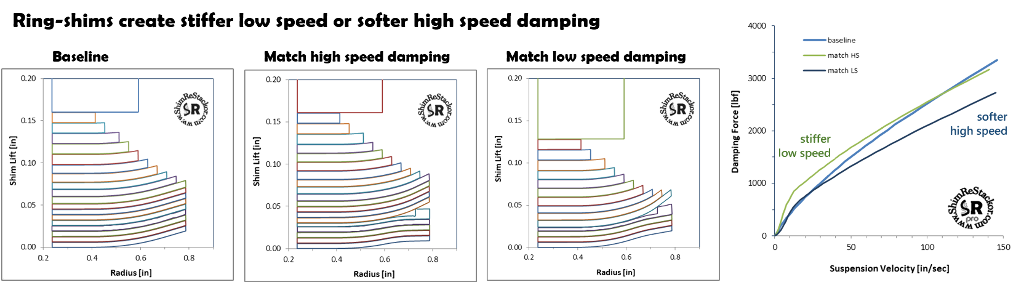
Face shim distortion
Ring-shim preload holds the outside edge of the shim stack closed. When used with thin face shims the clamped outside edge allows the face shims to distort and leak along the valve port side. The leak vents low speed damping partially defeating the purpose of the ring-shim.
That situation can be avoid using multiple or thicker face shims.
The stack deflection graphic in Shim ReStackor shows when the face shim stiffness is inadequate as the example below demonstrates.
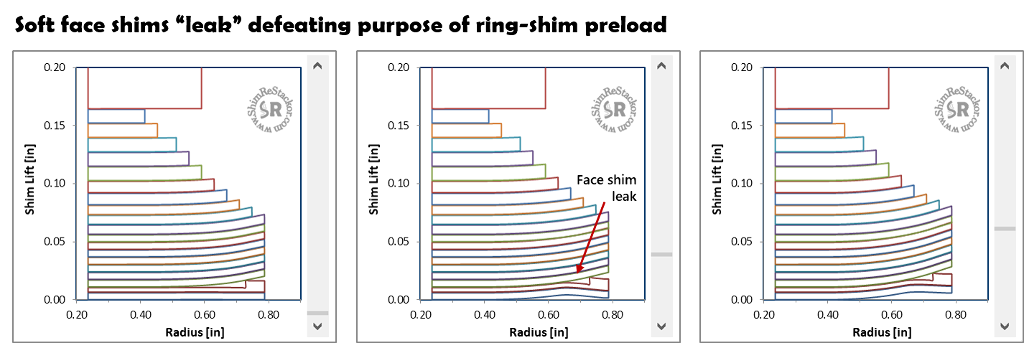
Shim stack float, entered in cell D6, allows the shim stack to physically lift off the valve face. Float makes the shim stack behave like a spring loaded check valve.
The check spring stiffness and preload entered in cells N6 through P6 control the float cracking pressure. When the shim stack lift reaches the float limit, the shim stack hits a hard stop. Damping force beyond that point is controlled by the shim stack deflection stiffness.
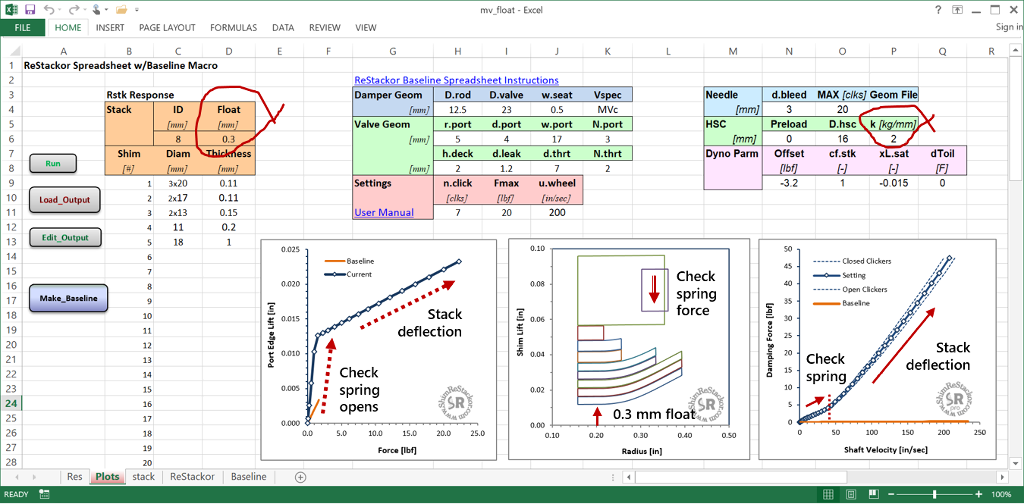
Float check spring
Shim ReStackor draws a small box on the shim diameter where the check spring force is applied to the shim stack. The check spring force can be applied at the clamp, the outside edge of the face shim,
or any arbitrary diameter on the shim stack taper. The typical configuration for a floated fork mid-valve applies the check spring force on the stack clamp washer.
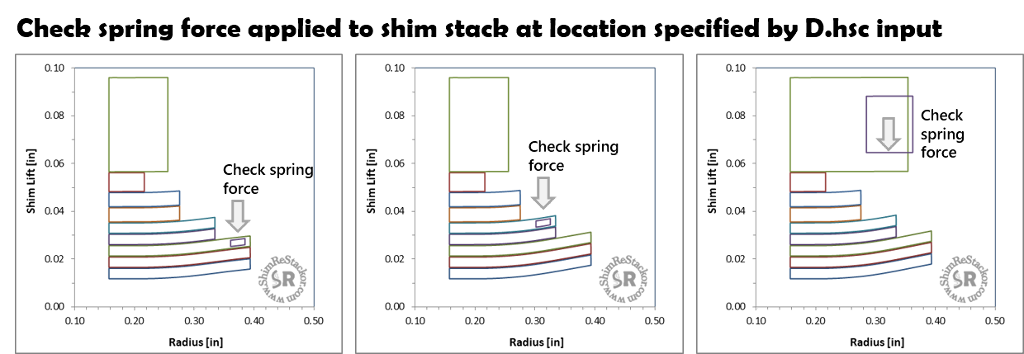
Low speed damping
Low speed damping is controlled by the float check spring stiffness and preload. Spring preload controls the cracking pressure and shock shaft velocity where float cracks open. Below that speed, damping is controlled by the bleed circuits.
The stiffness of the check spring controls the rate of float opening and damping force through the low speed range. At the end of float travel the shim stack hits a hard stop. Deflection of the shim stack controls damping beyond that point through the high speed range.
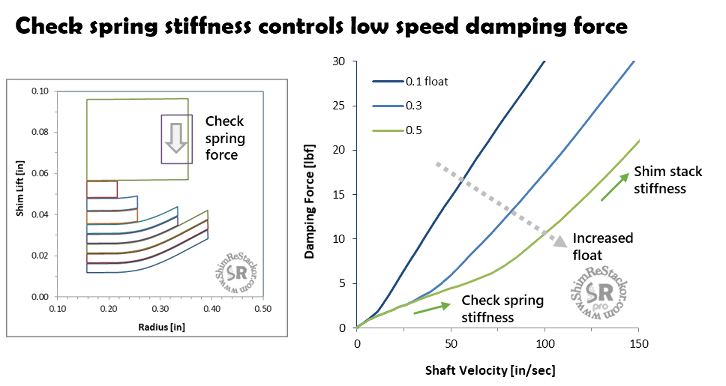
Shim stack float tuning
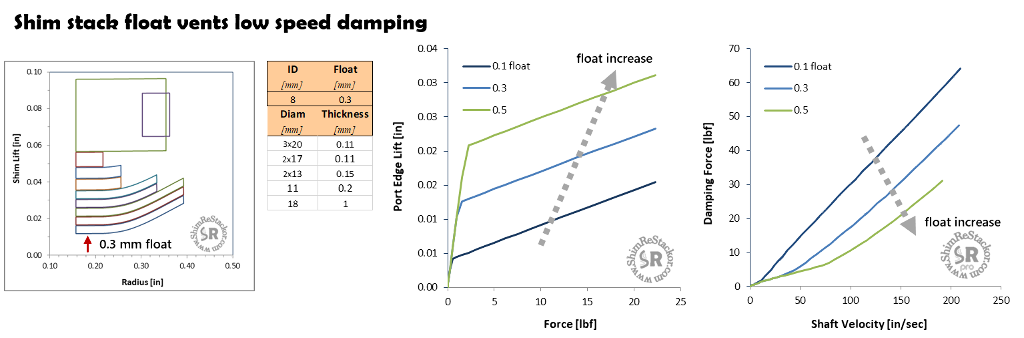
The combination of float, check spring stiffness, check spring preload and clicker bleed gives detailed control of damping force through the low speed range.
Shim ReStackor models all of those parameters making it easy to "see" the effect of each parameter, optimize the influance and control damping force across the entire range of suspension velocities.
Shim stack taper high speed damping force
The notion of the high speed stack controlling high speed damping is a widely spread myth.
A tapered stack, straight stack or stiff high speed stack can all be tuned to produce the same damping force curve.
Changing the clamp diameter or high speed stack stiffness clearly changes the shock absorber damping force and “feel” of the suspension. But, it does not change the shape of the damping force curve or the split between low and high speed damping.
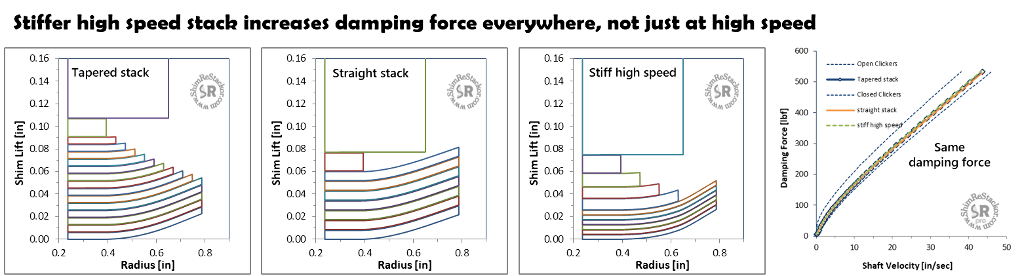
Tapered, straight and stiff high speed stack all produce the same damping force curve
Crossover shim stacks
Crossover shim stacks are the special case where the high speed stack makes a difference. Face shims control low speed damping and the combined high speed stack and face shims control high speed damping.
Installing a 20.15 mm crossover in the above shim stacks shows each stack produces a different damping force curve due to differences in the high speed stack stiffness.
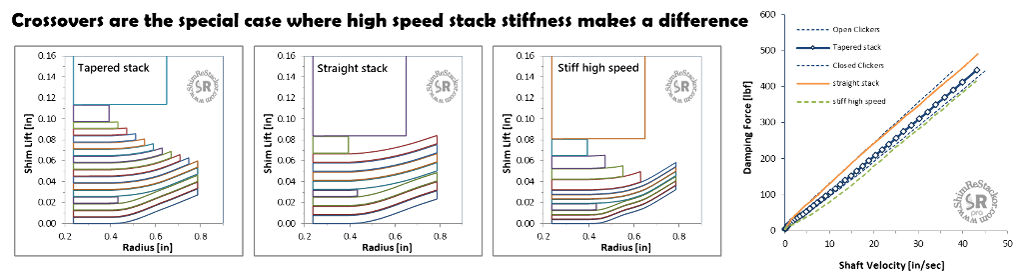
Stiffness of the high speed stack makes a difference in crossover shim stacks
Crossover tuning
However, the crossover in each of the shim stack configurations can be retuned to show the damping force is about the same for all three setups.
The example demonstrates there are often multiple shim stack configurations producing nearly identical damping force curves. The final configuration used is often simply based on the shims on hand at the time.
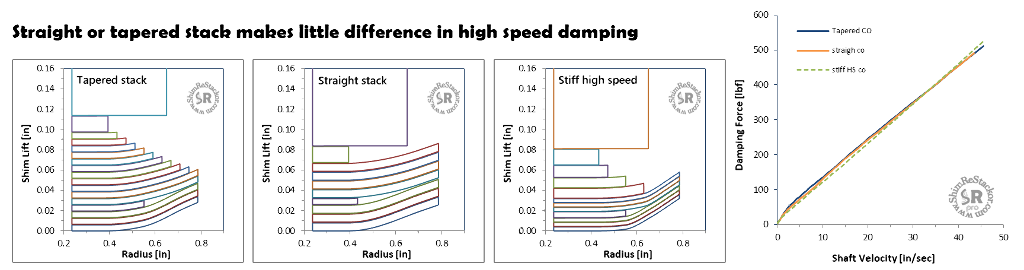
Multiple shim stack configurations can be tuned to produce nearly identical damping force curves

